Mathematical Definition

\[f(\mathbf{x}) = \sum_{i=1}^{n} \left [ \sum_{k=0}^{kmax} a^k \cos \left( 2 \pi b^k (x_i + 0.5) \right) - n \sum_{k=0}^{kmax} a^k \cos(\pi b^k) \right ] \]

where $a \in (0,1)$, $b$ is a positive odd integer, and $k_{max}$ is a positive integer (commonly $a=0.5$, $b=3$, $k_{max}=20$).

Plots

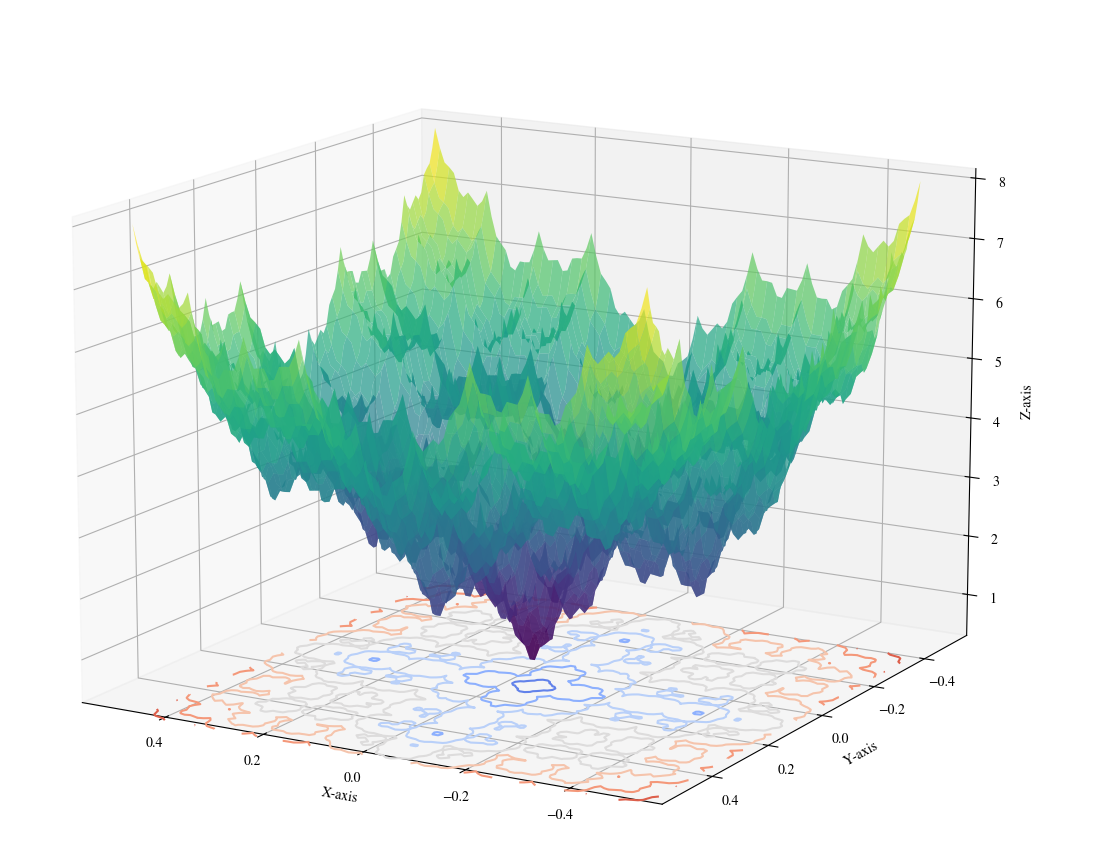
Description and Features

• The function is continuous but nowhere differentiable.
• The function is not convex.
• The function is defined on n-dimensional space.
• The function is multimodal.
• The function is separable.

Input Domain

The function is usually evaluated on the hypercube $x_i \in [-0.5, 0.5]$ for all $i = 1, …, n$.

Global Minimum

The global minimum is located at $\mathbf{x}^* = (0, …, 0)$, with

\[f(\mathbf{x}^*) = 0\]

Implementation

Python

For Python, the function is implemented in the benchmarkfcns package, which can be installed from command line with pip install benchmarkfcns.

from benchmarkfcns import weierstrass

print(weierstrass([[0, 0, 0],
                      [1, 1, 1]]))

MATLAB

An implementation of the Weierstrass Function with MATLAB is provided below.

% This function computes the Weierstrass function for each row of a matrix X,
% using a fully vectorized approach.
%
% Inputs:
%   X: A matrix where each row is a vector of dimension n.
%   a: A scalar parameter.
%   b: A scalar parameter.
%   kmax: An integer, the maximum value for k.
%
% Output:
%   y: A column vector where each element is the result for the corresponding row of X.
function y = weierstrassfcn(X, a, b, kmax)
    if nargin < 2
        a = 0.5;
    end
    if nargin < 3
        b = 3;
    end
    if nargin < 4
        kmax = 20;
    end

    [num_rows, n] = size(X);

    k = 0:kmax;

    k_reshaped = reshape(k, 1, 1, []); % 1x1x(kmax+1)

    X_reshaped = reshape(X + 0.5, num_rows, 1, n); % num_rows x 1 x n

    b_powers = b .^ k;

    term1_cos_input = 2 * pi * b_powers .* X_reshaped;
    term1 = a .^ k .* cos(term1_cos_input); % num_rows x (kmax+1) x n

    % Sum along the k dimension (the second dimension of term1)
    sum_k_term1 = sum(term1, 2); % num_rows x 1 x n

    sum_over_n = sum(sum_k_term1, 3); % num_rows x 1

    sum_k_term2 = sum(a .^ k .* cos(pi * b .^ k));

    y = sum_over_n - n * sum_k_term2;
end

The function can be represented in Latex as follows:

f(\mathbf{x}) = \sum_{i=1}^{n} \left [ \sum_{k=0}^{kmax} a^k \cos \left( 2 \pi b^k (x_i + 0.5) \right) - n \sum_{k=0}^{kmax} a^k \cos(\pi b^k) \right ] 

References

• Weierstrass function - Wikipedia
• Yao, X., Liu, Y., & Lin, G. (1999). Evolutionary programming made faster. IEEE Transactions on Evolutionary Computation, 3(2), 82-102.