Mathematical Definition

\[f(\mathbf{x})=f(x_1, ..., x_n)=\sum_{i=1}^{n}x_i^{10}\]

Plots

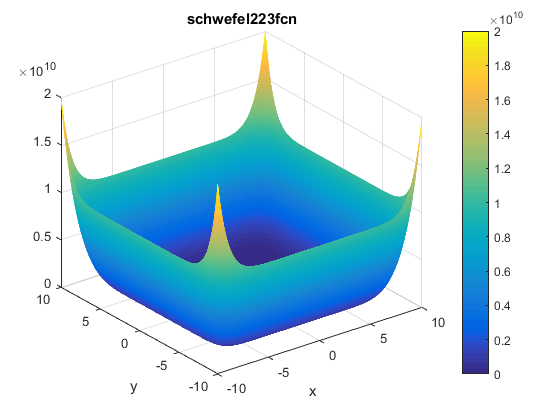
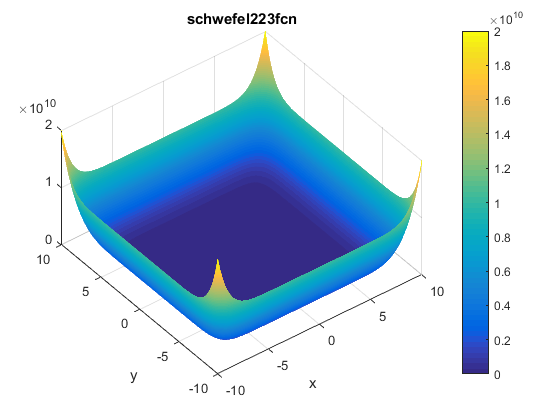
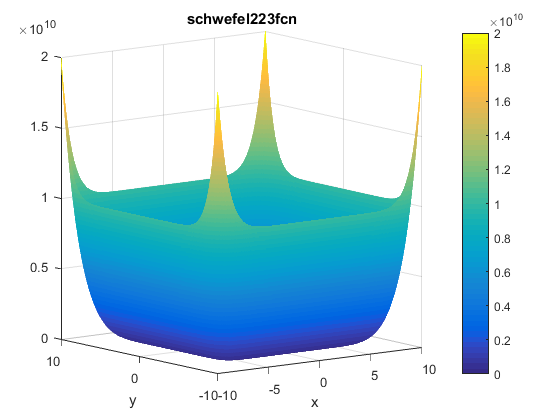
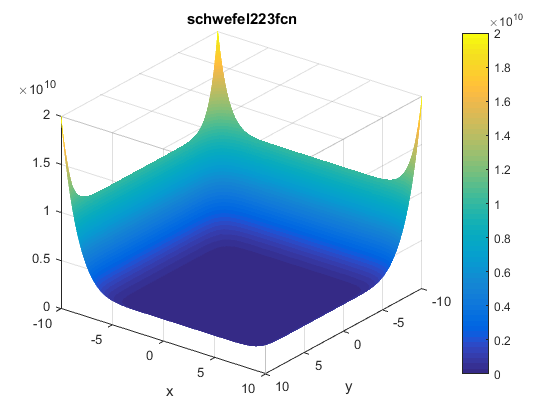
Contour of the function is presented below:

Description and Features

• The function is continuous.
• The function is convex.
• The function is defined on n-dimensional space.
• The function is unimodal.
• The function is non-differentiable.
• The function is separable.

Input Domain

Python

For Python, the function is implemented in the benchmarkfcns package, which can be installed from command line with pip install benchmarkfcns.

from benchmarkfcns import schwefel223

print(schwefel223([[0, 0, 0],
              [1, 1, 1]]))

MATLAB

The function can be defined on any input domain but it is usually evaluated on $x_i \in [-10, 10]$ for $i=1, …, n$.

Global Minima

The function has one global minimum $f(\textbf{x}^{\ast})=0$ at $\textbf{x}^{\ast} = (0, …, 0)$.

Implementation

An implementation of the Schwefel 2.23 Function with MATLAB is provided below.

% Computes the value of the Schwefel 2.23 function.
% SCORES = SCHWEFEL223FCN(X) computes the value of the Schwefel 2.23 
% function at point X. SCHWEFEL223FCN accepts a matrix of size M-by-N and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = schwefel223fcn(x)
    scores = sum(x .^10, 2);
end

The function can be represented in Latex as follows:

f(\mathbf{x})=f(x_1, ..., x_n)=\sum_{i=1}^{n}x_i^{10}

References:

• Momin Jamil and Xin-She Yang, A literature survey of benchmark functions for global optimization problems, Int. Journal of Mathematical Modelling and Numerical Optimisation}, Vol. 4, No. 2, pp. 150–194 (2013), arXiv:1308.4008
• H. P. Schwefel, “Numerical Optimization for Computer Models,” John Wiley Sons, 1981.