Mathematical Definition

\[f(x, y)=0.26(x^2+y^2) -0.48xy\]

Plots

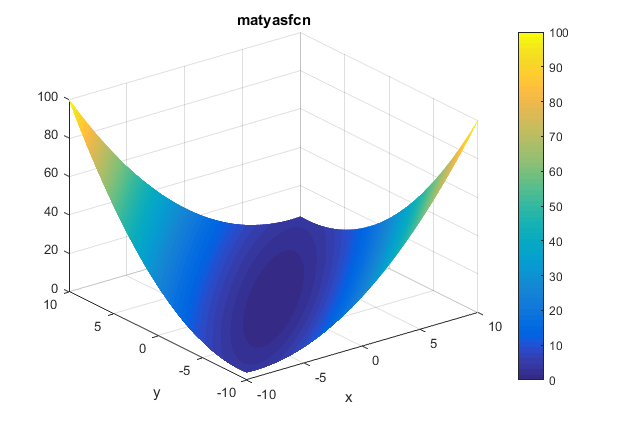
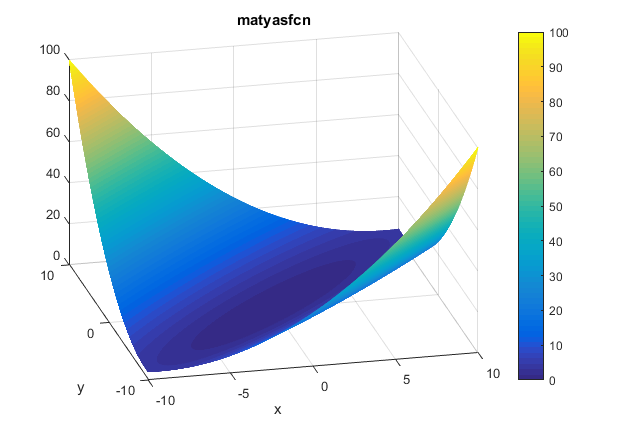
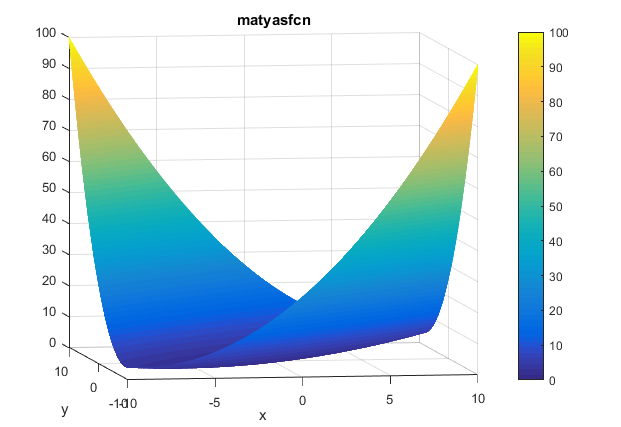
Matyas Function

Matyas Function

Matyas Function

The contour of the function is as presented below:

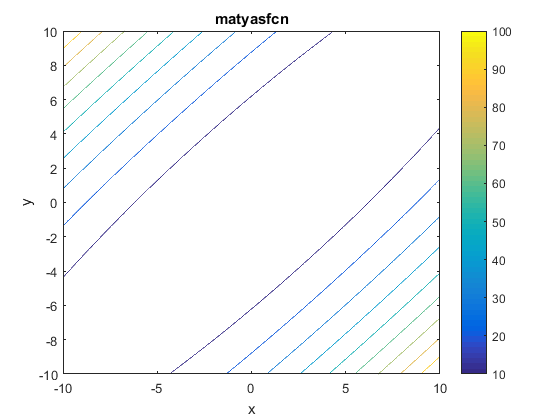
Matyas Function

Description and Features

  • The function is continuous.
  • The function is convex.
  • The function is defined on 2-dimensional space.
  • The function is unimodal.
  • The function is differentiable.
  • The function is non-separable.
  • The function is .

Input Domain

The function can be defined on any input domain but it is usually evaluated on $x \in [-10, 10]$ and $y \in [-10, 10]$ .

Global Minima

The function has one global minimum $f(\textbf{x}^{\ast})=0$ at $\textbf{x}^{\ast} = (0, 0)$.

Implementation

Python

For Python, the function is implemented in the benchmarkfcns package, which can be installed from command line with pip install benchmarkfcns.

from benchmarkfcns import matyas

print(matyas([[0, 0],
              [1, 1]]))

MATLAB

An implementation of the Matyas Function with MATLAB is provided below.

% Computes the value of the Matyas benchmark function.
% SCORES = MATYASFCN(X) computes the value of the Matyas function at 
% point X. MATYASFCN accepts a matrix of size M-by-2 and returns a  
% vetor SCORES of size M-by-1 in which each row contains the function value 
% for the corresponding row of X.
% For more information please visit: 
% https://en.wikipedia.org/wiki/Test_functions_for_optimization
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = matyasfcn(x)
    n = size(x, 2);
    assert(n == 2, 'Matyas''s function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    scores = 0.26 * (X .^ 2 + Y.^2) - 0.48 * X .* Y;
end

The function can be represented in Latex as follows:

f(x, y)=0.26(x^2+y^2) -0.48xy

References: