Mathematical Definition

\[f(\textbf{x})=\left[\left(||\textbf{x}||^2 - n\right)^2\right]^\alpha + \frac{1}{n}\left(\frac{1}{2}||\textbf{x}||^2+\sum_{i=1}^{n}x_i\right)+\frac{1}{2}\]

In the above definition, $\alpha$ is a real-valued parameter. For the value of $\alpha=\frac{1}{8}$, the contour of the function resembles a smiling cat, leading to the naming of the function.

Plots

For the value of $\alpha=1/8$, the function looks as:

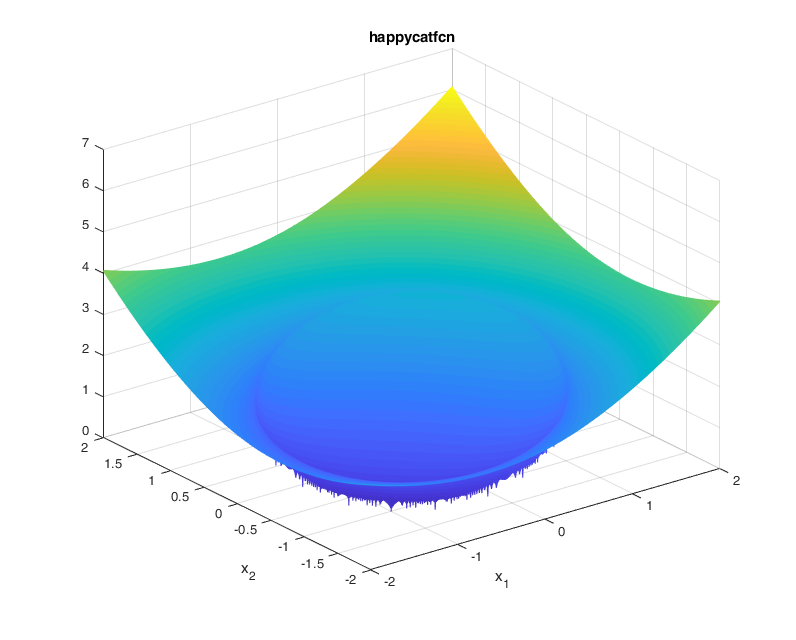
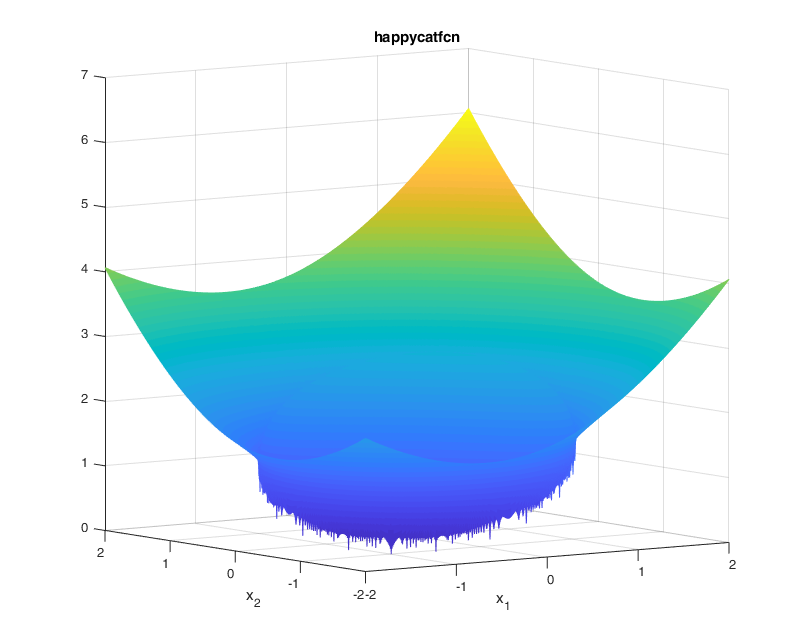
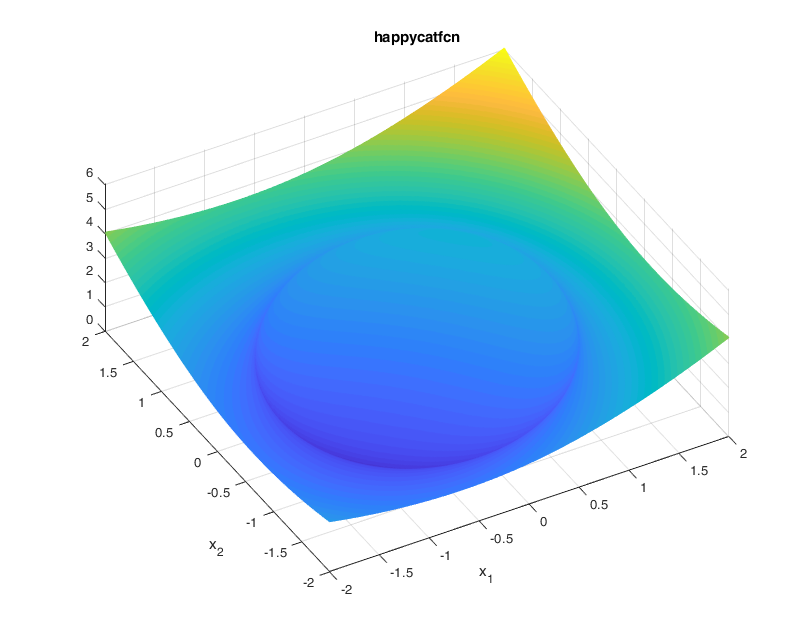
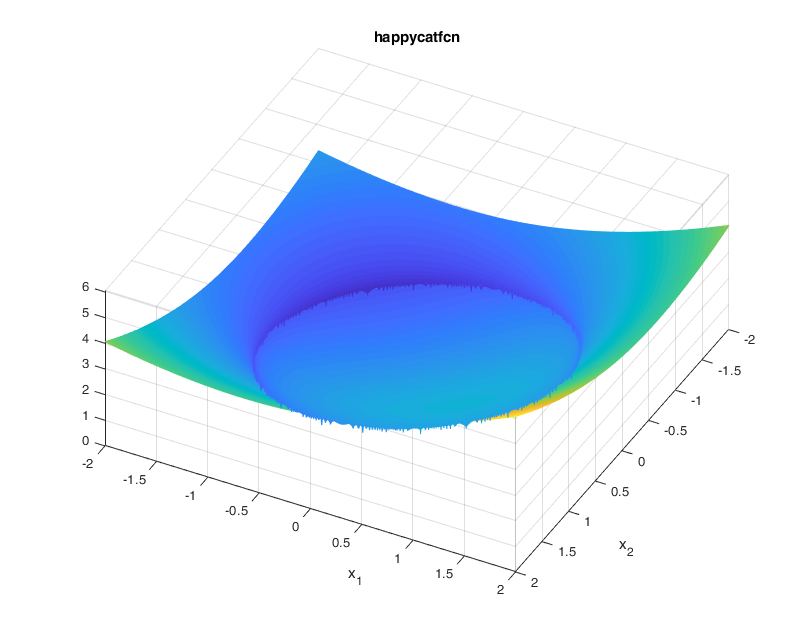
Happy Cat Function

A contour of the function is presented below:

Happy Cat Function

Description and Features

The function is not convex.
The function is defined on n-dimensional space.
The function is non-separable.
The function is differentiable.

Input Domain

The function can be defined on any input domain but it is usually evaluated on $x_i \in [-2, 2]$ for $i=1, …, n$.

Global Minima

The function has one global minimum at $f(\textbf{x}^{\ast}) = 0$ located at $\mathbf{x^\ast}=(-1, …, -1)$.

Implementation

Python

For Python, the function is implemented in the benchmarkfcns package, which can be installed from command line with pip install benchmarkfcns.

from benchmarkfcns import happycat

print(happycat([[0, 0, 0],
              [1, 1, 1]]))

MATLAB

An implementation of the Happy Cat Function with MATLAB is provided below.

% Computes the value of the Happy Cat benchmark function.
% SCORES = HAPPYCATFCN(X) computes the value of the Happy Cat function at 
% point X. HAPPYCATFCN accepts a matrix of size M-by-N and returns a vetor 
% SCORES of size M-by-1 in which each row contains the function value for 
% the corresponding row of X. 
% SCORES = HAPPYCAT(X, ALPHA) specifies power of the sphere component of 
% the function.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = happycatfcn(x, alpha)

    if nargin < 2 
        alpha = 0.5;
    end
    
    n = size(x, 2);
    x2 = sum(x .* x, 2);
    scores = ((x2 - n).^2).^(alpha) + (0.5*x2 + sum(x,2))/n + 0.5;
end

The function can be represented in Latex as follows:

f(\textbf{x})=\left[\left(||\textbf{x}||^2 - n\right)^2\right]^\alpha + \frac{1}{n}\left(\frac{1}{2}||\textbf{x}||^2+\sum_{i=1}^{n}x_i\right)+\frac{1}{2}

Acknowledgement:

Prof Hans-Georg Beyer kindly contributed the source code and literature for this function.

References:

Hans-Georg Beyer and Steffen Finck, HappyCat – A Simple Function Class Where Well-Known Direct Search Algorithms Do Fail, Parallel Problem Solving from Nature - PPSN XII, pp. 367–376 (2012), https://doi.org/10.1007/978-3-642-32937-1_37