Mathematical Definition

\[f(x,y)=|x^2 + y^2 + xy| + |sin(x)| + |cos(y)|\]

Plots

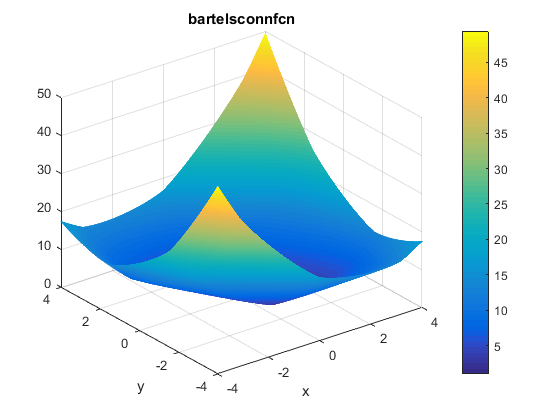
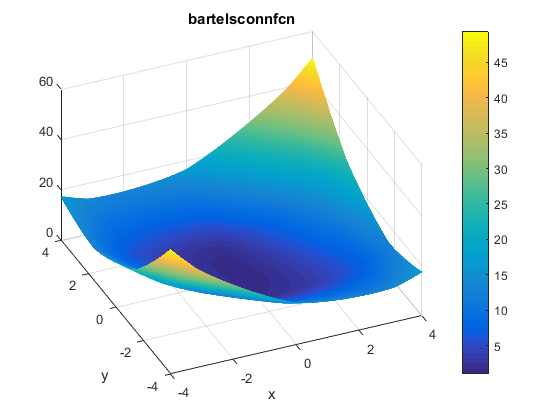
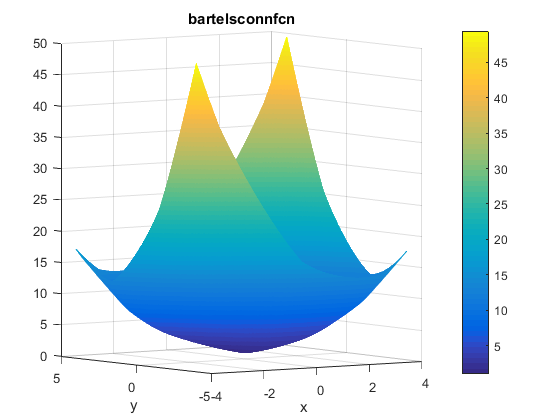
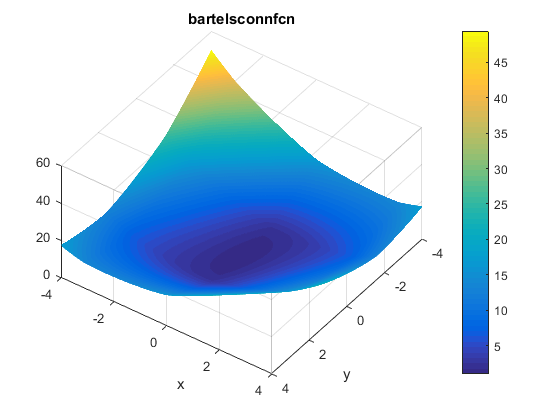
A contour of the function is presented below:

Description and Features

• The function is not convex.
• The function is defined on 2-dimensional space.
• The function is non-separable.
• The function is non-differentiable.

Input Domain

The function can be defined on any input domain but it is usually evaluated on $x \in [-500, 500]$ and $y \in [-500, 500]$.

Global Minima

The global minimum $f(\textbf{x}^{\ast})=1$ is located at $\mathbf{x^\ast}=(0, 0)$.

Implementation

Python

For Python, the function is implemented in the benchmarkfcns package and can be installed from command line with pip install benchmarkfcns.

from benchmarkfcns import bartelsconn

print(bartelsconn([[0, 0],
              [1, 1]]))

MATLAB

An implementation of the Bartels Conn Function with MATLAB is provided below.

% Computes the value of the Bartels Conn benchmark function.
% SCORES = BARTELSCONNFCN(X) computes the value of the Bartels Conn 
% function at point X. BARTELSCONNFCN accepts a matrix of size M-by-2 and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = bartelsconnfcn(x)
    
    n = size(x, 2);
    assert(n == 2, 'Bartels Conn function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    scores = abs((X .^ 2) + (Y .^ 2) + (X .* Y)) + abs(sin(X)) + abs(cos(Y));
end

The function can be represented in Latex as follows:

f(x,y)=|x^2 + y^2 + xy| + |sin(x)| + |cos(y)|

References:

• Momin Jamil and Xin-She Yang, A literature survey of benchmark functions for global optimization problems, Int. Journal of Mathematical Modelling and Numerical Optimisation}, Vol. 4, No. 2, pp. 150–194 (2013), arXiv:1308.4008