Mathematical Definition

\[f(\mathbf x)=f(x_1, ..., x_n) = \prod_{i=1}^{n}\sqrt{x_i}sin(x_i)\]

Plots

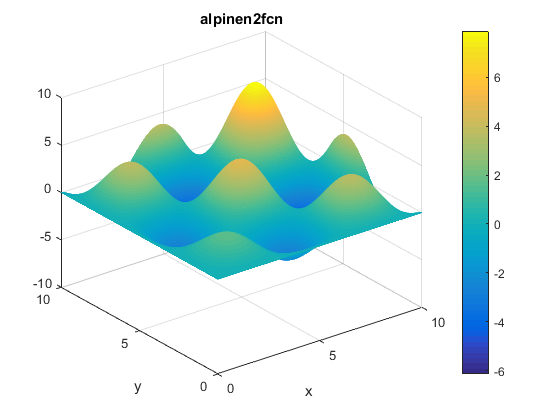
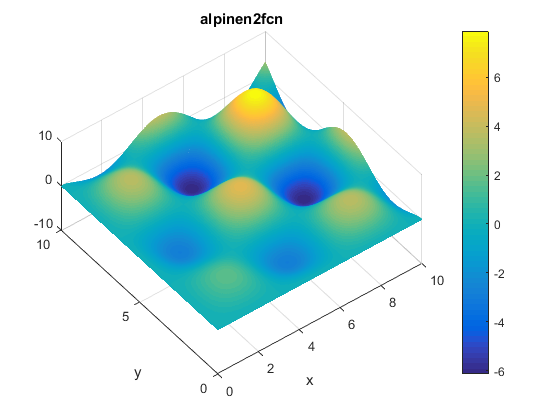
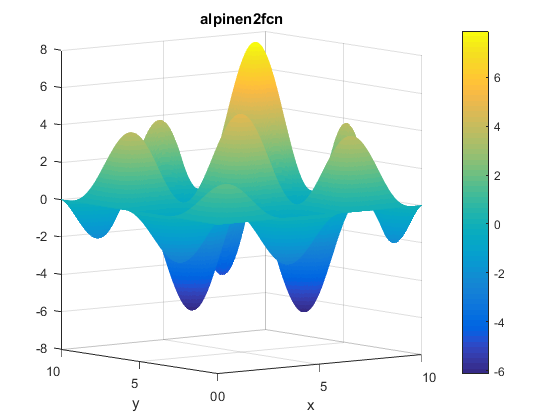
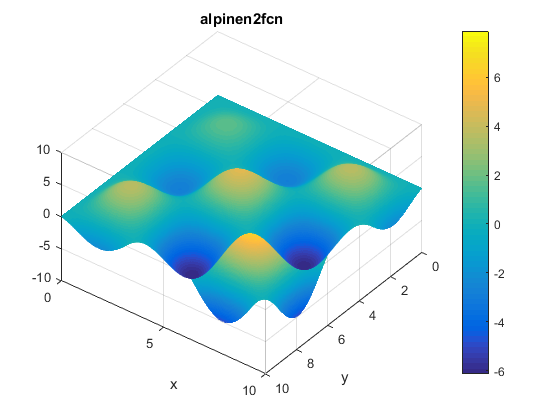
Alpine N. 2 Function

Alpine N. 2 Function

Alpine N. 2 Function

Alpine N. 2 Function

A contour of the function is presented below:

Alpine N. 2 Function

Description and Features

  • The function is not convex.
  • The function is defined on n-dimensional space.
  • The function is non-separable.
  • The function is differentiable.

Input Domain

The function can be defined on any positive input domain but it is usually evaluated on $x_i \in [0, 10]$ for $i=1, …, n$.

Global Minima

The function was devised By Clerc as a maximization problem and hence, the orginial paper gave $f(\textbf{x}^{\ast})=2.808^n$, located at $\mathbf{x^\ast}=(7.917, …, 7.917)$, as its global maximum. The function can be used for minization by negating its value.

Implementation

Python

For Python, the function is implemented in the benchmarkfcns package and can be installed from command line with pip install benchmarkfcns.

from benchmarkfcns import alpine2

print(alpine2([[0, 0, 0],
              [1, 1, 1]]))

MATLAB

An implementation of the Alpine N. 2 Function with MATLAB is provided below.

% Computes the value of the Alpine N. 2 function.
% SCORES = ALPINEN2FCN(X) computes the value of the Alpine N. 2
% function at point X. ALPINEN2FCN accepts a matrix of size M-by-N and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = alpinen2fcn(x)
     scores = prod(sqrt(x) .* sin(x), 2);
end

The function can be represented in Latex as follows:

f(\mathbf x)=f(x_1, ..., x_n) = \prod_{i=1}^{n}\sqrt{x_i}sin(x_i)

See Also:

References:

  • Momin Jamil and Xin-She Yang, A literature survey of benchmark functions for global optimization problems, Int. Journal of Mathematical Modelling and Numerical Optimisation}, Vol. 4, No. 2, pp. 150–194 (2013), arXiv:1308.4008
  • M. Clerc, “The Swarm and the Queen, Towards a Deterministic and Adaptive Particle Swarm Optimization, ” IEEE Congress on Evolutionary Computation, Washington DC, USA, pp. 1951-1957, 1999.