Ackley N. 4 Function
Mathematical Definition
\[f(\textbf{x})=\sum_{i=1}^{n-1}\left( e^{-0.2}\sqrt{x_i^2+x_{i+1}^2} + 3\left( cos(2x_i) + sin(2x_{i+1}) \right) \right)\]Plots
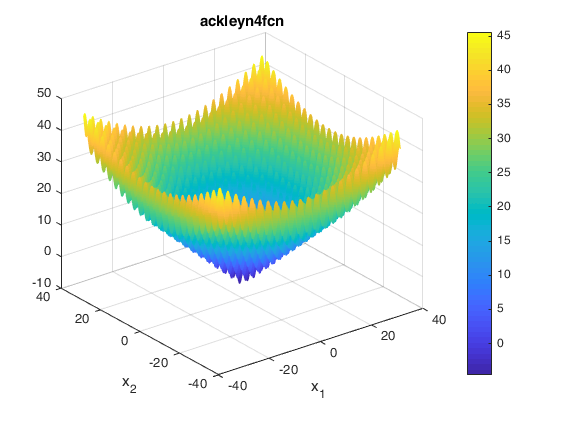
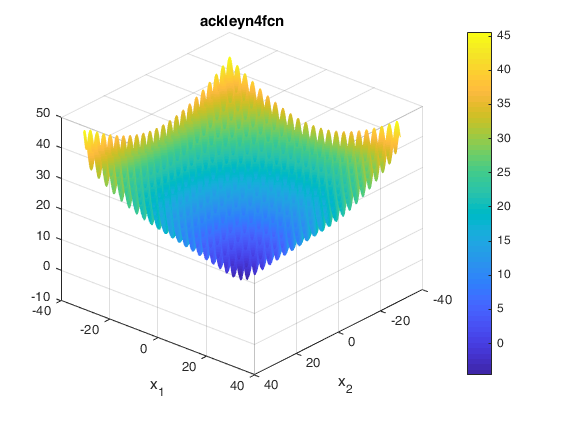
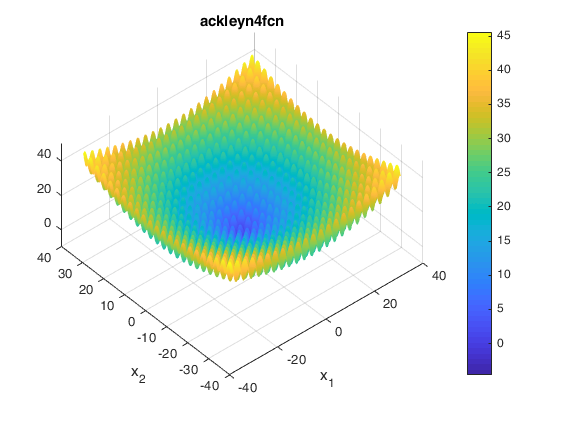
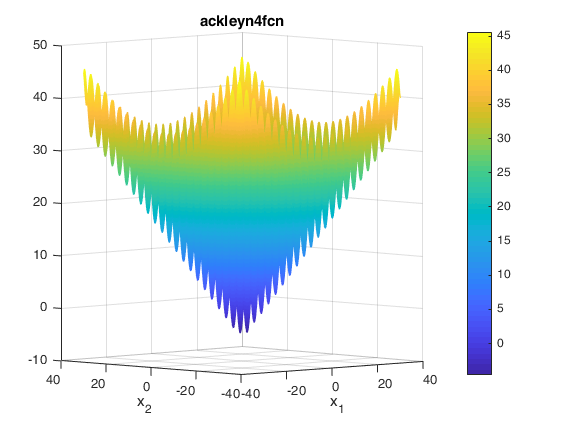
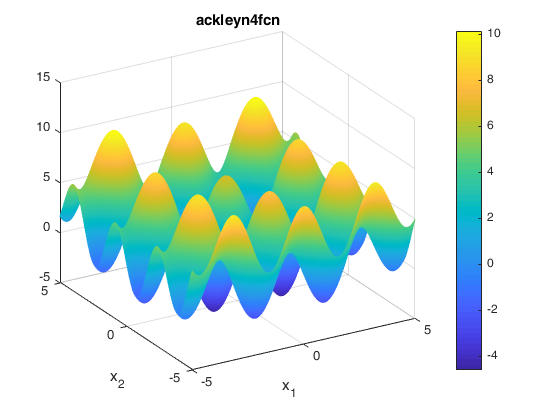
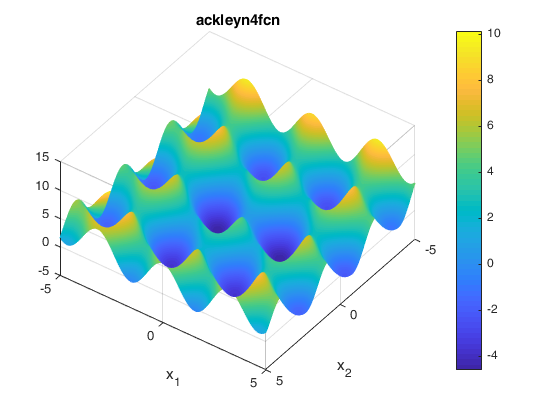
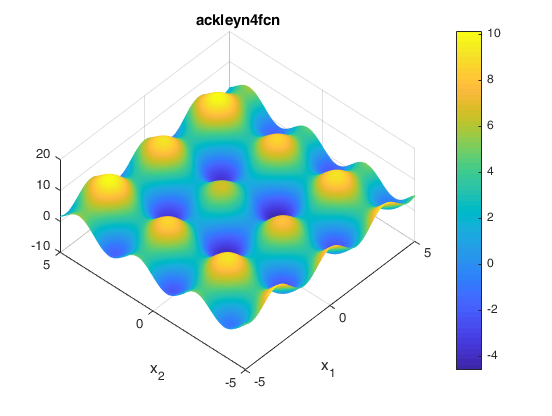
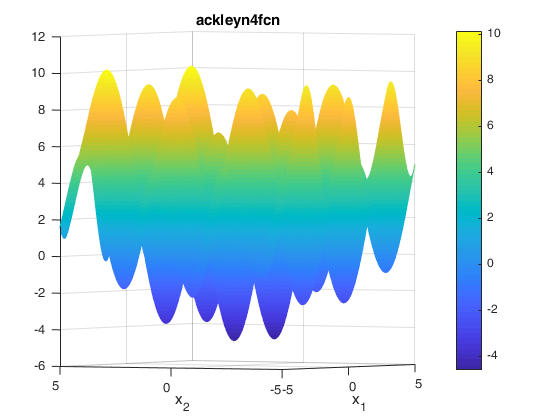
Two contours of the function are presented below:
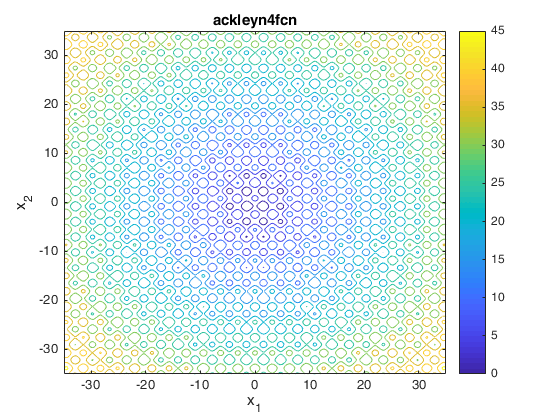
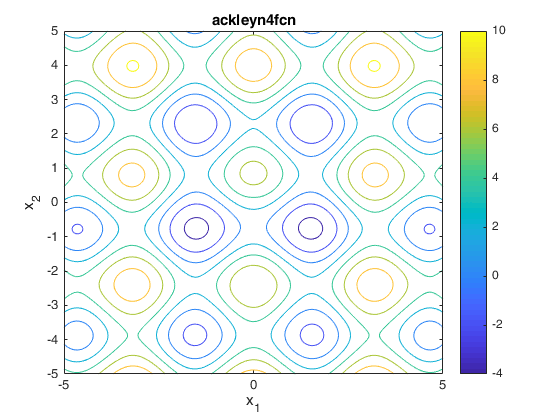
Description and Features
- The function is not convex.
- The function is defined on n-dimensional space.
- The function is non-separable.
- The function is differentiable.
Input Domain
The function can be defined on any input domain but it is usually evaluated on $x_i \in [-35, 35]$ for $i=1, …, n$.
Global Minima
On the 2-dimensional space, the function has one global minima at $f(\textbf{x}^{\ast}) = -4.590101633799122$ located at $\mathbf{x^\ast}=(-1.51, -0.755)$.
Implementation
Python
For Python, the function is implemented in the benchmarkfcns package and can be installed from command line with pip install benchmarkfcns.
from benchmarkfcns import ackley4
print(ackley4([[0, 0, 0],
[1, 1, 1]]))MATLAB
An implementation of the Ackley N. 4 Function with MATLAB is provided below.
% Computes the value of Ackley N. 4 benchmark function.
% SCORES = ACKLEYN4FCN(X) computes the value of the Ackey function at point
% X. ACKLEYN4FCN accepts a matrix of size M-by-N and returns a vetor SCORES
% of size M-by-1 in which each row contains the function value for each row
% of X.
%
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = ackleyn4fcn(x)
[m, n] = size(x);
scores = zeros(m, 1);
for i = 1:m
for j = 1:(n - 1)
scores = scores + exp(-0.2) .* sqrt( x(i, j) .^ 2 + x(i, j + 1) .^ 2 ) ...
+ 3 * ( cos(2 * x(i, j)) + sin(2 * x(i, j + 1)) );
end
end
endThe function can be represented in Latex as follows:
f(\textbf{x})=\sum_{i=1}^{n-1}\left( e^{-0.2}\sqrt{x_i^2+x_{i+1}^2} + 3\left( cos(2x_i) + sin(2x_{i+1}) \right) \right)See also:
References:
- Momin Jamil and Xin-She Yang, A literature survey of benchmark functions for global optimization problems, Int. Journal of Mathematical Modelling and Numerical Optimisation}, Vol. 4, No. 2, pp. 150–194 (2013), arXiv:1308.4008