Mathematical Definition

\[f(x, y) = -200e^{-0.2\sqrt{x^2 + y^2}} + 5e^{cos(3x) + sin(3y)}\]

Plots

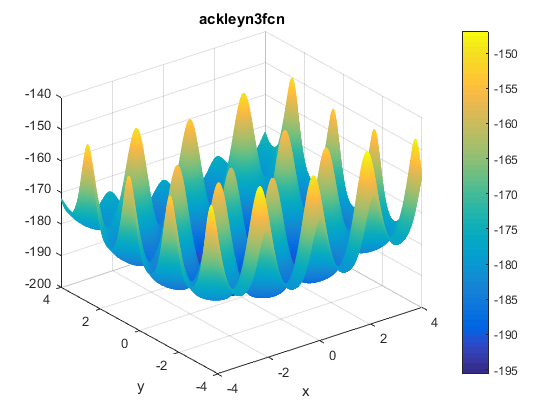
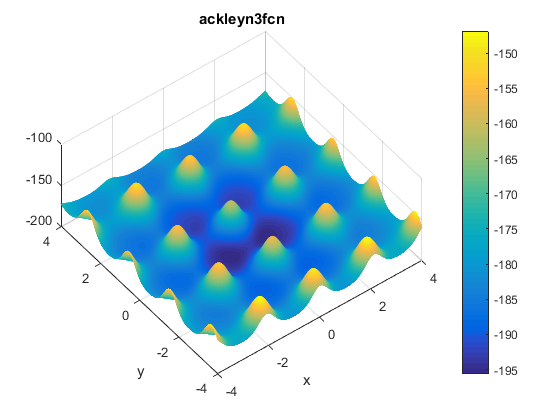
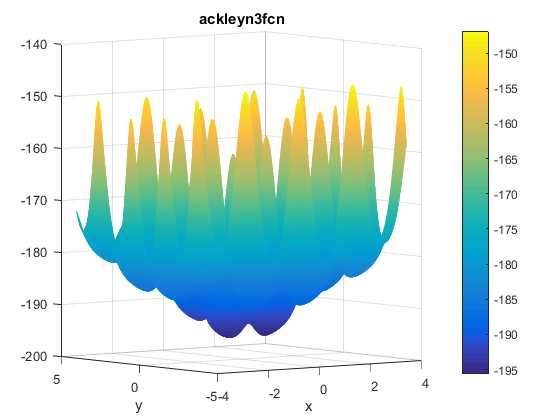
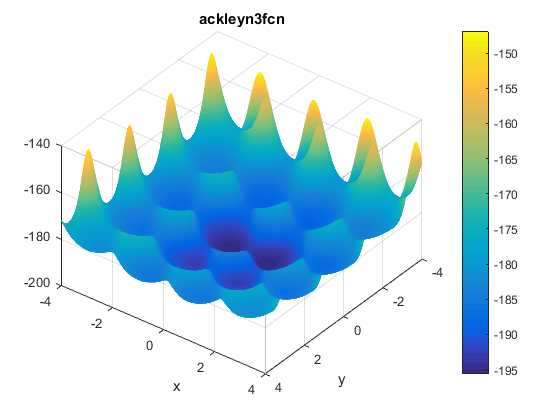
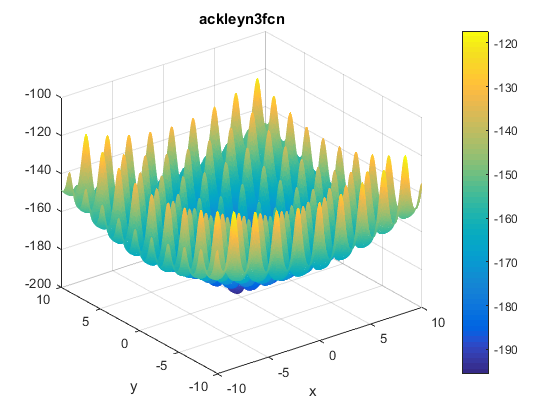
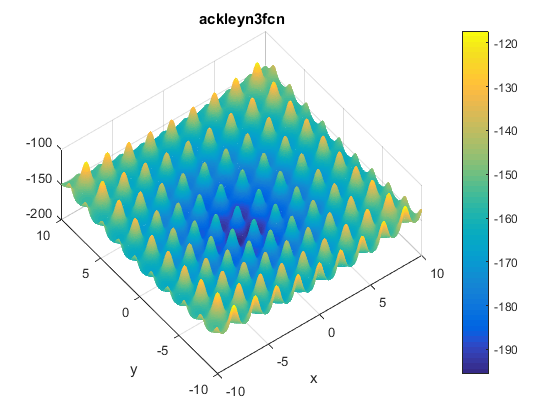
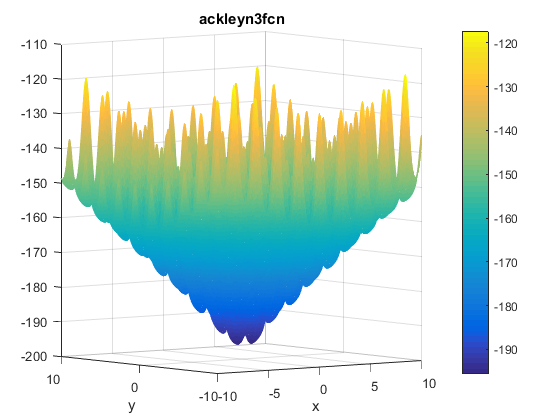
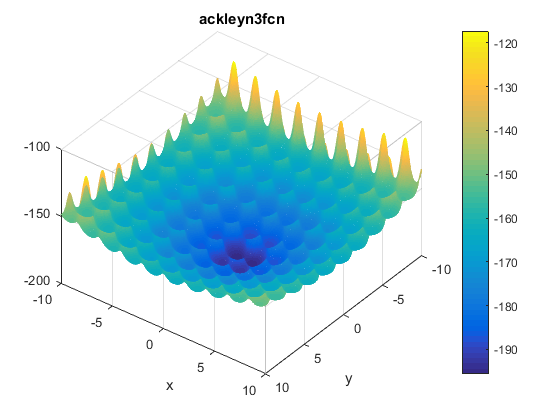
Two contours of the function are presented below:

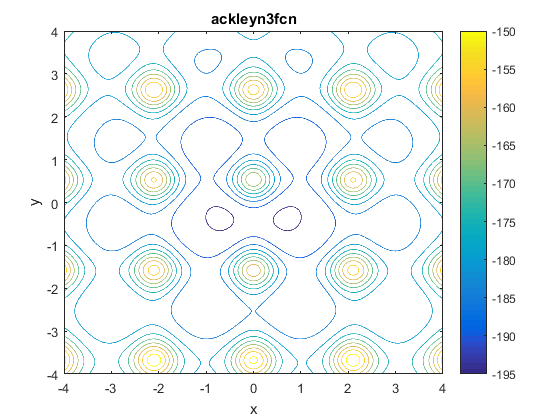
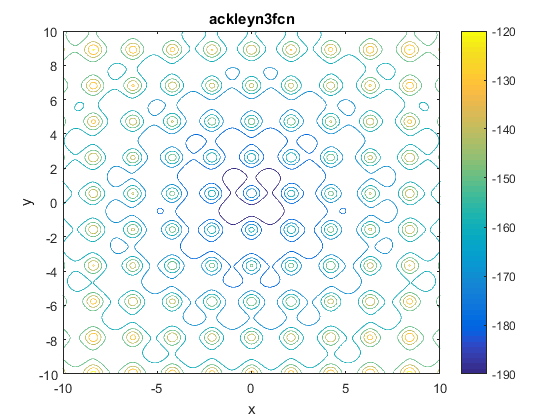
Description and Features

• The function is not convex.
• The function is defined on 2-dimensional space.
• The function is non-separable.
• The function is differentiable.

Input Domain

The function can be defined on any input domain but it is usually evaluated on $x_i \in [-32, 32]$ for $i=1, 2$.

Global Minima

The function has two global minima at $f(\textbf{x}^{\ast})\approx -195.629028238419$ located at $\mathbf{x^\ast}=(\pm0.682584587365898, -0.36075325513719)$.

Note: Minima values are obtained with Genetic Algorithm and may not be accurate.

Implementation

Python

For Python, the function is implemented in the benchmarkfcns package and can be installed from command line with pip install benchmarkfcns.

from benchmarkfcns import ackley3

print(ackley3([[0, 0],
              [1, 1]]))

MATLAB

An implementation of the Ackley N. 3 Function with MATLAB is provided below.

% Computes the value of the Ackley N. 3 function.
% SCORES = ACKLEYN3FCN(X) computes the value of the Ackley N. 3
% function at point X. ACKLEYN3FCN accepts a matrix of size M-by-2 and 
% returns a vetor SCORES of size M-by-1 in which each row contains the 
% function value for the corresponding row of X.
% 
% Author: Mazhar Ansari Ardeh
% Please forward any comments or bug reports to mazhar.ansari.ardeh at
% Google's e-mail service or feel free to kindly modify the repository.
function scores = ackleyn3fcn(x)
    
    n = size(x, 2);
    assert(n == 2, 'Ackley N. 3 function is only defined on a 2D space.')
    X = x(:, 1);
    Y = x(:, 2);
    
    scores = -200 * exp(-0.2 * sqrt((X .^ 2) + (Y .^ 2))) + ...
             5 * exp(cos(3 * X) + sin(3 * Y));
end

The function can be represented in Latex as follows:

f(x, y) = -200e^{-0.2\sqrt{x^2 + y^2}} + 5e^{cos(3x) + sin(3y)}

Acknowledgement

Yann Chern Jou kindly helped with the correctness of this document and helped discover a bug in the code.

See Also:

• Ackley Function
• Ackley N. 2 Function

References:

• Momin Jamil and Xin-She Yang, A literature survey of benchmark functions for global optimization problems, Int. Journal of Mathematical Modelling and Numerical Optimisation}, Vol. 4, No. 2, pp. 150–194 (2013), arXiv:1308.4008
• D. H. Ackley, “A Connectionist Machine for Genetic Hill-Climbing,” Kluwer, 1987.
• Nayak B., Dash S.K., Sahu J.B. (2019) Validation of Well-Known Population-Based Stochastic Optimization Algorithms Using Benchmark Functions. In: Bansal J., Das K., Nagar A., Deep K., Ojha A. (eds) Soft Computing for Problem Solving. Advances in Intelligent Systems and Computing, vol 816. Springer, Singapore